The lognormal model and the linearization effect
The lognormal is the simplest model of the structure-function exponents in turbulence: It predicts quadratic exponents. However, a quadratic function is not a realistic model for turbulence. This post discusses how a minimum Holder exponent changes this picture, linearizes the lognormal model, and may resolve this contradiction.
I. Brief review of multifractal theory
Parisi and Frisch proposed the multifractal theory in 1985 to describe the fluctuations of the dissipation field in turbulence. The dissipation field is not smooth (i.e., rough) in space, and one can assign a different Holder exponent at every point. Multifractal theory is the probabilistic description of this.
Suppose one coarse-grains a three-dimensional rough field at a scale $\ell$. The probability of observing a Holder exponent $h$ under this coarse-graining is
\[P(h,\ell) \propto \ell^{3-D(h)} .\]The function $D(h)$ is called the (multifractal) spectrum of singularities and is a concave function. It is equivalent to the fractal dimension of a set of exponent $h$.
Now consider some scale-dependent observable of a spatial field $u$. A simple one is the velocity increment,
\[\delta_{\ell} u(x) = u(x+\ell) - u(x) ,\]since they are conspicuous in turbulence theory, another example would be a wavelet coefficient.
At each point with Holder exponent $h$, increments show statistically self-similar behavior, that is,
\[\delta_{\ell} u \overset{d}{=} \sigma \, \ell^h ,\]where $\sigma$ is some unspecified random variable. The notation $\overset{d}{=}$ means that both sides follow the same statistical distribution. The exact distribution of $\sigma$ is unimportant in this discussion since we are only looking at the scaling behavior of the velocity increment.
Then, we compute statistical moments of the increments (also called structure functions) as
\[\langle (\delta_{\ell} u)^n \rangle = \frac{\langle \sigma^n \rangle}{Z(\ell)} \int dh \, \ell^{3-D(h)+nh},\]with the normalization
\[Z(\ell) = \int dh \, \ell^{3-D(h)} .\]In the limit of small scales, this integral can be computed with a saddle-point approximation, and we obtain the following scaling behavior:
\[\langle (\delta_{\ell} u)^n \rangle \underset{\ell \to 0^+}{\sim} c_n \, \ell^{\zeta_n},\]where the exponents are
\[\zeta_n = \min_h \left( 3-D(h) + n h \right) .\]The notation $\sim$ means asymptotic equivalence.
II. Monofractal fields have linear exponents
For many multifractal fields, it’s observed that the exponents $\zeta_n$ linearize at large values of $n$. This first example is of a field whose exponents are always linear.
The simplest rough fields are not multifractal; they are fractal (or monofractal). This is the case for the fractional Gaussian field. In three dimensions, its spectrum of exponents is
\[D(h) = \begin{cases} 3, &\text{if $h = \beta$,} \\ -\infty, &\text{otherwise}, \end{cases}\]where $\beta$ is the Holder exponent of the field everywhere in space.
To compute the scaling exponents of this model, we’ll use a saddle point method. If $h_0$ is a minimum of $S(h)$, contained in the integration domain, and $S\prime\prime(h_0) > 0$, then the following asymptotic integral can be computed with the saddle point method:
\[\int dh \, f(h) e^{-\lambda S(h)} \underset{\lambda \to \infty}{\sim} \sqrt{\frac{2\pi}{\lambda |S''(h_0)|}} f(h_0) \, e^{- \lambda S(h_0)}.\]Using the saddle point method, we obtain
\[Z(\ell) \underset{\ell \to 0^+}{\sim} 1,\]and
\[\langle (\delta_{\ell} u)^n \rangle \underset{\ell \to 0^+}{\sim} \ell^{3-D(\beta) + \beta n} = \ell^{\beta n} .\]That is, the scaling exponents of a monofractal field are linear and equal to
\[\zeta_n = \beta n.\]III. The lognormal model
The simplest turbulence model is K41 (meaning Kolmogorov 1941), which says that a turbulent field is monofractal, with $\beta = 1/3$. Soon after, experimental observations showed that this was incorrect and that the incompressible Navier-Stokes scaling exponents are not linear. The next simplest model proposed was the lognormal, with a quadratic spectrum of exponents:
\[D(h) = 3 - \frac{(h-c_1)^2}{2c_2} .\]To be clear, these theories were reformulated only later in terms of the multifractal model. Parisi and Frisch first studied multifractals in 1985, while Kolmogorov and Obukhov proposed the lognormal model in 1962.
Let’s compute the scaling exponents of the lognormal model. We’ll also do a saddle point approximation in the limit $\ell \to 0^+$. The integral we are computing is
\[\langle (\delta_{\ell} u)^n \rangle = \frac{\langle \sigma^n \rangle}{Z(\ell)} \int_{\mathbb{R}} dh \, \ell^{3-D(h)+nh}.\]Starting with the denominator: Its exponent is
\[S(h) = \frac{(h-c_1)^2}{2c_2},\]with a minimum at $h_Z = c_1$. The saddle-point integral is then
\[Z(\ell) \underset{\ell \to 0^+}{\sim} \sqrt{\frac{2\pi c_2}{|\log \ell|}}.\]For the numerator, the exponent is now
\[S(h) = \frac{(h-c_1)^2}{2c_2} + nh,\]which has a minimum at
\[h_n = c_1 - n c_2.\]The concavity at the minimum is
\[S''(h_n) = 1 / c_2,\]which is positive; hence, it is a non-degenerate minimum.
Since the lognormal model is quadratic, these integrals can be computed exactly, matching the asymptotic formulas. Nevertheless, the saddle-point model is more versatile and can be used where analytical solutions are unavailable.
Collecting the numerator and denominator, we obtain
\[\langle (\delta_{\ell} u)^n \rangle \underset{\ell \to 0^+}{\sim} \langle \sigma^n \rangle \, \ell^{3-D(h_n) + n h_n},\]which gives an exponent
\[\zeta_n = 3 - D(h_n) + n h_n = c_1 n - \frac{c_2}{2} n^2.\]The exponents are also quadratic and are not far from those observed in numerical simulations. In Ref. 2, they were measured to be close to $c_1 = 0.37$ and $c_2 = 0.025$. With these values, notice that $\zeta_3 = 1$: This is, so far, the only non-trivial structure function exponent that can be computed directly from the Navier-Stokes equations.
The lognormal model is better than the linear one, but some things still need to be fixed.
One of them is that the exponents $\zeta_n$ must be concave and non-decreasing – this is a requirement of the incompressibility condition (for a proof, see Ref. 1, Chap. 8.4). As we can see, $\zeta_n$ is increasing for $n < c_1/c_2$, and then starts to decrease.
The other issue is the linearization of the exponents at large values of $n$: This effect was first observed by Molchan (Refs. 3 and 4), and is incompatible with the lognormal model. The following section will show how to resolve these issues while keeping the lognormal model.
IV. A better lognormal model
The spectrum of exponents describes how Holder exponent $h$ structures are distributed in the flow. In the last section, no bounds were imposed on $h$, but is it plausible to expect large negative values?
The Holder exponent describes the regularity (i.e., smoothness) of the field: It is at least one for smooth fields, $0 < h < 1$ for continuous but nondifferentiable fields, and $h=0$ represents discontinuities. Negative exponents, then, mean singularities. There is no proof that the solution of the Navier-Stokes equations is continuous, but based on numerical simulations, they seem to be. Then, let’s restrict the exponents to be in the range $h_{\min} < h < h_{\max}$, with $h_{\min} > 0$. The new spectrum of exponents is
\[D(h) = \begin{cases} 3 - \frac{(h-c_1)^2}{2c_2}, &\text{if $h_{\min} < h < h_{\max}$,} \\ -\infty, &\text{otherwise.} \end{cases}\]The structure functions, in this case, are
\[\langle (\delta_{\ell} u)^n \rangle = \frac{\langle \sigma^n\rangle}{Z(\ell)} \int_{h_{\min}}^{h_{\max}} dh \, \ell^{3-D(h)+nh},\]which can be computed with the saddle-point method as well.
The denominator is precisely the same as before if $h_{\min} \leq c_1 \leq h_{\max}$, which is plausible.
The numerator, on the other hand, is the same only if $h_{\min} < h_n < h_{\max}$. Since $h_n$ is a decreasing function of $n$, at some point it goes below $h_{\min}$. In this case, the minimum of the exponent is at $h_{\min}$ and no longer at $h_n$. Then, the saddle-point approximation returns
\[\zeta_n = 3 - D(h_{\min}) + n h_{\min},\]which is linear in $n$. Since $h_{\min} > 0$, it also happens that we never reach the case of decaying exponents, $c_1/c_2 < n$; the linearization avoids this.
One can also extrapolate to the case of large negative exponents, where $h_n > h_{\max}$, and the linearization shows up again, with exponents
\[\zeta_n = 3 - D(h_{\max}) + n h_{\max}.\]To conclude, the lognormal model with a maximum and minimum Holder exponent gives us
\[\zeta_n = \begin{cases} 3 - D(h_{\max}) + n h_{\max} \ &\text{if $n < (c_1-h_{\max})/c_2$} \\ c_1 n - c_2 n^2/2 \ &\text{if $(c_1-h_{\max})/c_2 \leq n \leq (c_1 - h_{\min})/c_2$,} \\ 3 - D(h_{\min}) + n h_{\min} \ &\text{if $n > (c_1-h_{\min})/c_2$}. \end{cases}\]As a last comparison, let’s look at the Beta model (Ref 5). It predicts linear scaling exponents as well:
\[\zeta_p = p/3 + (3-d)(1-p/3)\](Ref. 1, Eq 8.37). In this equation, $d$ corresponds to the spatial dimension of the monofractal structures in the model, which are almost space-filling at approximately $d=2.8$ (see Ref. 6).
Matching the coefficients in $p$ for the lognormal and Beta models, we can solve for $d$ and $h_{\min}$, obtaining
\[h_{\min} = c_1 - 3 c_2,\]and
\[d = 2 + 3 c_1 - 9 c_2.\]Together with the estimates of Chevillard et al., the numerical values are $h_{\min} \approx 0.3$ and $d \approx 2.9$.
A few interesting remarks about these values are:
- The value of $d$ is very close to the independently measured value of 2.8.
- The value of $h_{\min}$ is compatible with Onsager’s theorem, which requires structures with Holder exponent $h \leq 1/3$ so that there is dissipation without viscosity. (See Ref. 7)
- This correspondence predicts that the transition from lognormal to linear happens at $n = (c_1 - h_{\min})/c_2 = 3$. This is a property of the Beta model since it has $\zeta_3 = 1$ and we require $\zeta_n$ to be continuous.
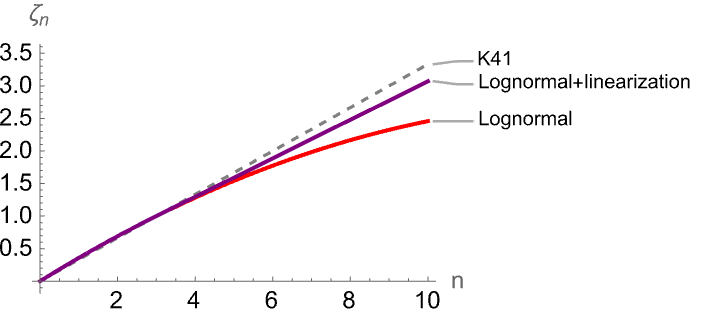
The next figure compares three models: The linear model (K41) in gray, the lognormal model without bounds on the Holder exponent in red, and the lognormal model with linearization in purple.
References
- Frisch, U. (1995). Turbulence: the legacy of A. N. Kolmogorov. Cambridge University Press.
- Chevillard, L., Castaing, B., Arneodo, A., Lévêque, E., Pinton, J. F., & Roux, S. G. (2012). A phenomenological theory of Eulerian and Lagrangian velocity fluctuations in turbulent flows. Comptes Rendus Physique, 13(9-10), 899-928.
- G. M. Molchan, Scaling exponents and multifractal dimensions for independent random cascades, Comm. Math. Phys. 179 (3) (1996) 681–702.
- G. M. Molchan, Turbulent cascades: limitations and a statistical test of the lognormal hypothesis, Phys. Fluids 9 (8) (1997) 2387–2396
- Frisch, U., Sulem, P. L., & Nelkin, M. (1978). A simple dynamical model of intermittent fully developed turbulence. Journal of Fluid Mechanics, 87(4), 719-736.
- De Rosa, L., & Isett, P. (2024). Intermittency and lower dimensional dissipation in incompressible fluids. Archive for Rational Mechanics and Analysis, 248(1), 11.
- Eyink, G. L., & Sreenivasan, K. R. (2006). Onsager and the theory of hydrodynamic turbulence. Reviews of modern physics, 78(1), 87.